A matemática é repleta de padrões fascinantes e sequências intrigantes, e entre essas, a sequência de Fibonacci se destaca como uma das mais belas e misteriosas.
Descoberta por Leonardo de Pisa, também conhecido como Fibonacci, no século XIII (13), essa sequência tem cativado matemáticos, cientistas e entusiastas por séculos.
Neste artigo, exploraremos o que é a sequência de Fibonacci, seu significado matemático e suas diversas aplicações no mundo real.
Veja também: Curiosidades sobre a evolução humana: descobrindo nossas raízes
O que é a Sequência de Fibonacci?
A sequência de Fibonacci é uma série de números em que cada número é a soma dos dois anteriores. Começando com 0 e 1, a sequência se desenvolve da seguinte forma: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, e assim por diante. Formalmente, a sequência de Fibonacci pode ser definida pela relação de recorrência F(n)=F(n−1)+F(n−2)F(n)=F(n−1)+F(n−2), onde F(0)=0F(0)=0 e F(1)=1F(1)=1.
A beleza matemática da Sequência de Fibonacci
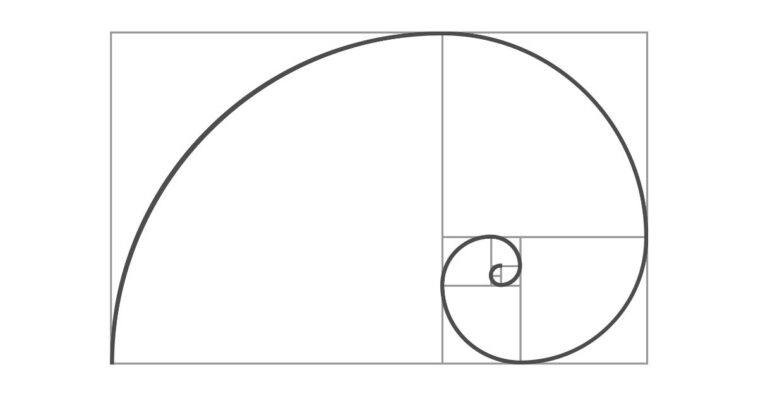
Os números de Fibonacci são notáveis por sua abundância de padrões e propriedades matemáticas intrigantes. Uma das propriedades mais surpreendentes é a proporção áurea, também conhecida como número de ouro (ϕϕ).
À medida que os números de Fibonacci aumentam, a razão entre um número e seu anterior se aproxima de ϕϕ, que é aproximadamente 1,61803398875. Essa proporção é considerada esteticamente agradável e é frequentemente encontrada em arte, arquitetura e natureza, incluindo conchas, flores e galáxias.
Veja também: Curiosidades sobre a História da Medicina
Aplicações da Sequência de Fibonacci
Mesmo que você tenha achado complicado compreender tantos números, com certeza já viu a sequência de Fibonacci em várias aplicações práticas em diversos campos, desde ciência da computação até biologia e finanças.
Algoritmos e Ciência da Computação
Essa sequência numérica é frequentemente usada em algoritmos e programação. Algoritmos que envolvem recursão, como o cálculo de números de Fibonacci, são comuns em ciência da computação. Além disso, a sequência é usada em técnicas como a busca binária e em algoritmos de ordenação.
Modelagem em Biologia

A biologia também encontra utilidade nessa sequência numérica. Por exemplo, o padrão de crescimento em espiral das conchas de moluscos e a forma como as flores organizam suas pétalas muitas vezes seguem padrões relacionados à sequência de Fibonacci.
Veja também: 14 Dicas de estudo eficientes para alunos de todas as idades
Mercado Financeiro
Os traders de mercado frequentemente aplicam níveis de retração de Fibonacci para identificar pontos de suporte e resistência em gráficos de preços de ativos, ajudando a tomar decisões informadas sobre negociações.
Arquitetura e Arte

Arquitetos e artistas utilizam a proporção áurea derivada da sequência de Fibonacci para criar designs visualmente harmoniosos. Edifícios famosos, como a Parthenon na Grécia, foram construídos com base em princípios relacionados à sequência de Fibonacci.
Teoria das Filas
Em teoria das filas, um campo da matemática aplicada, esse padrão pode ser usado para modelar padrões de chegada de clientes em sistemas de filas, ajudando a otimizar a eficiência do atendimento ao cliente em diversas indústrias.
Em resumo
Com sua rica história e amplas aplicações, essa sequência continua a intrigar e inspirar pessoas em todo o mundo. Sua presença em várias disciplinas, desde a matemática pura até a aplicada, demonstra a incrível relevância dessa sequência numérica.
À medida que exploramos mais profundamente os mistérios da matemática e aplicamos esses conhecimentos em várias áreas, os números de Fibonacci permanecerão como uma lembrança duradoura da maravilha matemática que existe no coração do nosso mundo.
Veja também: 9 Enigmas não resolvidos da Ciência